Skip to content

피드포워드 신경망과 역전파

개요

이 포스팅에서는 역전파 알고리즘을 사용하여 피드포워드 신경망을 훈련하는 방법을 설명한다. 뉴런, 가중치, 편향, 활성화 함수, 손실 함수 등 신경망의 기본 개념과 용어도 설명한다. 이 포스팅에서 간단한 피드포워드 신경망을 Python으로 구현하고 분류 문제를 해결하는 데 사용할 수 있다.

피드포워드 신경망은 가장 널리 사용되는 인공 신경망 타입 중 하나이다. 이들은 입력 데이터에 대한 수학적 연산을 수행하고 출력을 생성하는 상호 연결된 노드, 즉 뉴런의 여러 레이어로 구성되어 있다. 피드포워드 신경망은 충분한 데이터와 계산 자원이 주어지면 어떤 함수의 근사치를 학습할 수 있다. 이들은 종종 이미지 인식, 자연어 처리 및 음성 합성 같은 작업에 사용된다.

역전파 알고리즘은 피드포워드 신경망이 데이터로부터 학습하고 그에 따라 매개변수를 조정할 수 있도록 하는 알고리즘이다. 네트워크 출력의 오류, 즉 손실을 계산하여 네트워크를 통해 역전파하고, 그 과정에서 각 뉴런의 가중치와 편향을 업데이트한다는 개념이다. 역전파는 미적분학의 연쇄 법칙을 응용한 것으로, 단순한 구성 요소의 도함수(derivatives)를 곱하여 복잡한 함수의 도함수를 계산할 수 있다.

이 포스팅을 따라가려면 Python과 데이터 분석에 대한 기본적인 이해가 필요하다. 또한 다음과 같은 라이브러리를 설치해야 한다.

  • NumPy: 배열 작업과 과학 컴퓨팅을 위한 라이브러리
  • Matplotlib: 데이터를 플롯하고 시각화하기 위한 라이브러리
  • Scikit-learn: 기계 학습과 데이터 마이닝을 위한 라이브러리

pip 명령을 사용하여 이 라이브러리를 설치할 수 있다.

# Install the libraries
$ pip install numpy matplotlib scikit-learn

피드포워드 신경망과 역전파가 어떻게 작동하는지 배울 준비가 되었나요? 시작해 봅시다!

피드포워드 신경망이란?

피드포워드 신경망은 입력 데이터를 처리하여 출력을 생성하는 노드, 즉 뉴런의 여러 레이어로 구성된 인공 신경망의 일종이다. 피드포워드란 데이터가 피드백 루프나 사이클 없이 입력 레이어에서 출력 레이어로 한 방향으로 흐르는 것을 의미한다. 피드포워드 신경망은 방향성 비순환 그래프(DAG, directed acyclic graph)로 표현될 수 있다. 여기서 각 노드는 뉴런을 나타내고 각 엣지는 뉴런 간의 연결을 나타낸다.

뉴런(neuron)은 신경망에서 계산의 기본 단위이다. 하나 이상의 입력을 받아 가중치 합을 수행하고 바이어스 항을 추가한 후 비선형 활성화 함수를 적용하여 출력을 생성한다. 가중치와 바이어스는 뉴런이 입력에 어떻게 반응하는지를 결정하는 매개 변수이다. 활성화 함수는 비선형성을 네트워크에 도입하여 복잡한 패턴과 함수를 학습할 수 있도록 하는 수학적 함수이다.

피드포워드 신경망은 입력 레이어와 출력 레이어 사이에 하나 이상의 은닉 레이어를 가질 수 있다. 은닉 레이어는 외부 데이터와 직접 연결되어 있지는 않지만 입력 데이터에 대한 중간 연산과 변환을 수행한다. 네트워크의 복잡성과 용량은 은닉 레이어의 수와 크기에 따라 결정된다. 은닉 레이어와 뉴런이 더 많은 네트워크는 더 복잡한 기능을 학습할 수 있지만, 훈련하기 위해서는 더 많은 데이터와 계산 자원이 필요하다.

피드포워드 신경망의 출력 레이어는 네트워크의 최종 출력을 생성한다. 이는 단일 값일 수도 있고 값의 벡터일 수도 있다. 출력 레이어는 네트워크가 해결하려는 문제의 타입에 따라 다른 활성화 함수를 가질 수 있다. 예를 들어, 네트워크가 연속적인 값을 예측하려고 하는 회귀 문제의 경우, 출력 레이어는 선형 활성화 함수를 가질 수 있다. 네트워크가 입력에 이산 레이블을 할당하려고 하는 분류 문제의 경우, 출력 레이어는 softmax 활성화 함수를 가질 수 있으며, 이는 가능한 클래스에 대한 확률 분포를 생성한다.

다음 그림은 하나의 입력 레이어, 하나의 은닉 레이어와 하나의 출력 레이어를 갖는 피드포워드 신경망의 예를 나타낸다. 각 원은 뉴런을 나타내고, 각 화살표는 가중치를 갖는 연결을 나타낸다. 다이어그램에는 바이어스 항이 표시되어 있지 않다.

# Import the libraries
import numpy as np
import matplotlib.pyplot as plt

# Define the network architecture
input_size = 2 # Number of input neurons
hidden_size = 3 # Number of hidden neurons
output_size = 2 # Number of output neurons

# Define the network parameters
W1 = np.array([[0.1, 0.2, 0.3], [0.4, 0.5, 0.6]]) # Weights from input to hidden layer
b1 = np.array([0.7, 0.8, 0.9]) # Biases of hidden layer
W2 = np.array([[0.1, 0.2], [0.3, 0.4], [0.5, 0.6]]) # Weights from hidden to output layer
b2 = np.array([0.7, 0.8]) # Biases of output layer

# Define the activation functions
def sigmoid(x):
    # Sigmoid function
    return 1 / (1 + np.exp(-x))

def softmax(x):
    # Softmax function
    exp_x = np.exp(x)
    return exp_x / np.sum(exp_x, axis=1, keepdims=True)

# Define the input data
X = np.array([[0, 0], [0, 1], [1, 0], [1, 1]]) # Input data matrix
y = np.array([[0, 1], [1, 0], [1, 0], [0, 1]]) # Output data matrix

# Plot the input data
plt.scatter(X[:, 0], X[:, 1], c=np.argmax(y, axis=1), cmap=plt.cm.coolwarm)
plt.xlabel('x1')
plt.ylabel('x2')
plt.title('Input data')
plt.show()

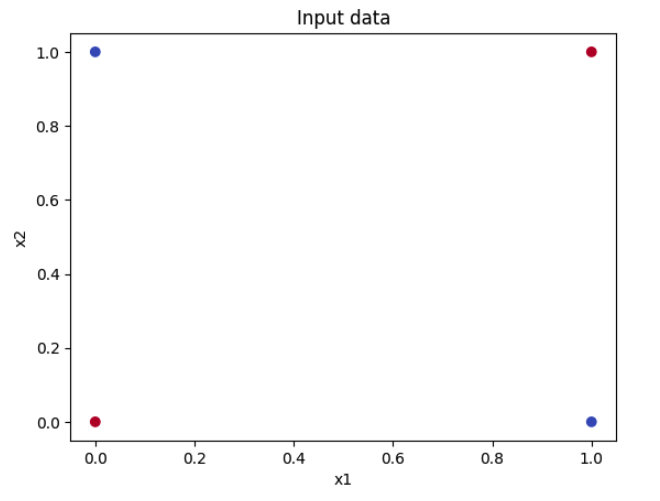
그림은 입력 데이터를 보여주며, 각 점은 \(\mathbf{x}_1\)과 \(\mathbf{x}_2\) 두 개의 피처을 가진 입력 벡터를 나타낸다. 점의 색상은 출력 클래스인 0 또는 1을 나타낸다.

네트워크의 출력을 계산하려면 다음 단계를 포함하는 순방향 패스를 수행해야 한다.

  • 입력 데이터 행렬 \(\mathbb{X}\)에 가중치 행렬 \(\mathbb{W}_1\)을 곱하고 바이어스 벡터 \(\mathbf{b}_1\)을 더하여 은닉층 입력 \(\mathbb{Z}_1\)을 얻는다.
  • 시그모이드 활성화 함수를 \(\mathbb{Z}_1\)에 적용하여 은닉층 출력 \(\mathbb{A}_1\)을 얻는다.
  • 은닉레이어 출력 \(\mathbb{A}_1\)에 가중치 행렬 \(\mathbf{W}_2\)를 곱하고 바이어스 벡터 \(\mathbf{b}_2\)를 더하여 출력 레이어 입력 \(\mathbb{Z}_2\)를 얻는다.
  • 네트워크의 최종 출력인 출력레이어 출력 \(\mathbb{A}_2\)를 얻기 위하여 softmax 활성화 함수를 \(\mathbb{Z}_2\)에 적용한다.

다음 코드는 Python에서 순방향 패스를 수행하는 방법을 보인다.

# Perform a forward pass
Z1 = X.dot(W1) + b1 # Hidden layer input
A1 = sigmoid(Z1) # Hidden layer output
Z2 = A1.dot(W2) + b2 # Output layer input
A2 = softmax(Z2) # Output layer output

# Print the output
print(A2)

출력은 4X2 형태의 행렬이며, 여기서 각 행은 각 입력 벡터에 대한 두 클래스에 대한 확률 분포를 나타낸다. 예를 들어, 첫 번째 행 [0.525, 0.475]는 네트워크가 입력 벡터 [0, 0]에 대해 첫 번째 클래스에 52.5%의 확률을 할당하고 두 번째 클래스에 47.5%의 확률을 할당한다는 것을 의미한다.

[[0.525 0.475]
 [0.524 0.476]
 [0.523 0.477]
 [0.522 0.478]]

보다시피, 네트워크는 예측에 대해 그다지 자신이 없으며, 모든 입력에 대해 두 클래스에 거의 동일한 확률을 할당한다. 네트워크가 아직 훈련되지 않았으며, 네트워크의 매개변수가 무작위로 초기화되기 때문이다. 네트워크를 훈련시키기 위해서는 역전파 알고리즘을 사용해야 하며, 이 알고리즘은 다음 절에서 설명할 것이다.

피드포워드 신경망의 동작

이 절에서는 입력 레이어 하나, 은닉 레이어 하나, 출력 레이어 하나로 구성된 단순한 네트워크의 예를 들어 피드포워드 신경망의 작동 원리를 설명한다. 네트워크의 구조와 계산을 설명하는 데 사용되는 수학적 표기법과 공식도 설명한다.

이 포스팅에서 사용할 몇 가지 기호와 변수를 정의하는 것부터 시작하겠다.

- \(n_x\): 입력 레이어에서 입력 뉴런 또는 피처 의 갯수

- \(n_h\): 은닉 레이어에서 은닉 뉴런의 갯수

- \(n_y\): 출력 레이어에서 출력 뉴런 또는 클래스의 갯수

- \(\mathbb{X}\): \(n_z\) x \(m\) 입력 데이터 행렬, \(m\)은 입력 데이터 세트에서 샘플 갯수

- \(y\): \(n_y\) x \(m\) 출력 데이터 행렬, 각 열은 해당 입력 벡터의 실제 레이블 또는 클래스를 표시한다.

- \(W^{[l]}\): 네트워크에서 \(l\) 레이어의 가중치 행렬, 위의 예에서 \(l\)은 1 또는 2이 될 수 있다. 가중치 행렬은 (\(n^{[l]}\), \(n^{[l-1]}\))이며, \(n^{[l]}\)은 레이어 \(l\)에서 뉴런의 갯수이며, \(n^{[l-1]}\)은 이전 레이어에서 뉴런의 갯수이다.

- \(b^{[l]}\): 네트워크에서 레이어 \(l\)의 편향 벡터, 위의 예에서 \(l\)은 1 또는 2이 될 수 있다. 편향 벡터는 (\(n^{[l]}\), 1)이며, \(n^{[l]}\)은 레이어 \(l\)에서 뉴런의 갯수이다.

- \(\mathbb{Z}^{[l]}\): 네트워크에서 레이어 \(ㅣ\)의 입력, 가중치 및 편향의 선형 결합으로 위의 예에서 \(l\)은 1 또는 2일 수 있다. 선형 결합은 (\(n^{[l]}\), m) 행렬으로, \(n^{[l]}\)은 레이어 \(l\)에서 뉴런의 갯수이며, \(m\)은 데이터 세트에서 샘플 갯수이다.

- \(\mathbb{A}^{[l]}\): 네트워크에서 레이어 \(l\)의 활성화 출력으로, 위의 예에서 \(l\)은 1 또는 2일 수 있다. 활성화 출력은 선형 결합 (\(n^{[l]}\), m)과 동일한 행렬 구조를 갖으며, \(n^{[l]}\)은 레이어 \(l\)에서 뉴런의 갯수이며, \(m\)은 데이터 세트에서 샘플 갯수이다.

- \(g^{[l]}\): 네트워크에서 레이어 \(l\)의 활성화 함수로 위의 예에서 \(l\)은 1 또는 2일 수 있다. 활성화 함수는 선형 결합을 sigmoid, tanh, relu 또는 softmax 같은 활성화 출력으로 맻핑하는 비선형 함수일 수 있다.

이 기호들과 변수들을 이용하여 네트워크의 순방향 패스에 대한 일반적인 공식을 작성할 수 있으며, 각 레이어에 대해 다음과 같은 두 단계로 구성된다.

- Step 1: 레이어의 입력, 가중치 및 편향의 선형 결합을 계산한다.

\[\mathbb{Z}^{[l]} = \mathbb{W}^{[l]}\mathbb{A}^{[l-1]}+b^{[l]}\]

- 레이어의 활성화 출력을 얻기위하여 활성화 함수를 선형 결합에 적용한다.

\[\mathbb{A}^{[l]} = g^{[l]}(\mathbb{Z}^{[l]})\]

첫 번째 레이어에서는 이전 레이어의 활성화 출력 \(\mathbb{A}^{[0]}\)으로 입력 데이터 행렬 \(\mathbb{X}\)를 사용한다. 또한, 최종 레이어의 활성화 출력 \(\mathbb{A}^{[L]}\)는 네트워크의 최종 출력 \(\hat{y}\)이다.

이제, 이 식을 입력 레이어 하나, 은닉 레이어 하나 및 출력 레이어 하나로 이루어진 예 네트워크에 적용하여 보자. 이전 절에서 사용하였던 입력 데이터 행렬 \(\mathbb{X}\)와 출력 데이터 행렬 \(y\)를 사용한다. 또한 동일한 가중치 행렬 \(\mathbb{W}^{[1]}\)과 \(\mathbb{W}^{[2]}\)를 사용하며, 앞 절에서 정의한 편행 벡터 \(b^{[1]}\)과 \(b^{[2]}\)를 사용한다. 은익 레이어에서는 활성화 함수로 sigmoid를 출력 레이어에서는 softmax 활성화 함수를 사용할 것이다.

다음 코드는 Python에서 네트워크의 순방향 패스를 수행하는 방법을 보인다.

# Import the libraries
import numpy as np
import matplotlib.pyplot as plt

# Define the network architecture
n_x = 2 # Number of input neurons
n_h = 3 # Number of hidden neurons
n_y = 2 # Number of output neurons

# Define the network parameters
W1 = np.array([[0.1, 0.2, 0.3], [0.4, 0.5, 0.6]]) # Weights from input to hidden layer
b1 = np.array([0.7, 0.8, 0.9]) # Biases of hidden layer
W2 = np.array([[0.1, 0.2], [0.3, 0.4], [0.5, 0.6]]) # Weights from hidden to output layer
b2 = np.array([0.7, 0.8]) # Biases of output layer

# Define the activation functions
def sigmoid(x):
    # Sigmoid function
    return 1 / (1 + np.exp(-x))

def softmax(x):
    # Softmax function
    exp_x = np.exp(x)
    return exp_x / np.sum(exp_x, axis=1, keepdims=True)

# Define the input data
X = np.array([[0, 0], [0, 1], [1, 0], [1, 1]]) # Input data matrix
y = np.array([[0, 1], [1, 0], [1, 0], [0, 1]]) # Output data matrix

# Perform a forward pass
Z1 = X.dot(W1) + b1 # Hidden layer input
A1 = sigmoid(Z1) # Hidden layer output
Z2 = A1.dot(W2) + b2 # Output layer input
A2 = softmax(Z2) # Output layer output

# Print the output
print(A2)

출력은 앞 절의 형태 4X2 행렬과 동일하며, 여기서 각 행은 각 입력 벡터에 대한 두 클래스에 대한 확률 분포를 나타낸다.

[[0.525 0.475]
 [0.524 0.476]
 [0.523 0.477]
 [0.522 0.478]]

이것이 피드포워드 신경망의 작동 원리이다. 입력된 데이터를 받아 여러 레이어의 뉴런에 전달하고, 각각 선형 조합과 비선형 활성화를 수행하여 네트워크의 최종 출력을 생성하는 출력 레이어에 도달한다. 다음 절에서는 역전파 알고리즘을 사용하여 네트워크를 훈련하는 방법에 대해 알아본다.

역전파란?

역전파 알고리즘은 피드포워드 신경망이 데이터로부터 학습하고 그에 따라 매개변수를 조정할 수 있도록 하는 알고리즘이다. 네트워크 출력의 오류, 즉 손실을 계산하여 네트워크를 통해 역전파하고, 그 과정에서 각 뉴런의 가중치와 편향을 업데이트한다는 개념이다. 역전파는 미적분학의 연쇄 법칙을 응용한 것으로, 복잡한 함수의 도함수를 단순한 구성 요소의 도함수를 곱하여 계산할 수 있다.

역전파의 목표는 네트워크의 출력이 실제 출력과 얼마나 잘 일치하는지를 측정하는 손실 함수를 최소화하는 것이다. 손실 함수는 네트워크가 해결하려는 문제의 종류에 따라 달라진다. 예를 들어 이진 분류 문제에 대해 우리는 이진 교차 엔트로피 손실 함수를 사용할 수 있는데, 이것을 다음과 같이 정의한다.

# Define the binary cross-entropy loss function
def binary_cross_entropy_loss(y_true, y_pred):
    # y_true is the true output data matrix
    # y_pred is the network output data matrix
    # m is the number of input vectors
    m = y_true.shape[0]
    # Compute the loss for each input vector
    loss = - (y_true * np.log(y_pred) + (1 - y_true) * np.log(1 - y_pred))
    # Compute the average loss over all input vectors
    loss = np.sum(loss) / m
    return loss

이진 교차 엔트로피 손실 함수는 참 출력 데이터 행렬 \(\mathbb{y}\)(y_true)와 네트워크 출력 데이터 행렬 \(\hat{y}\)(y_pred)를 입력으로 하고 모든 입력 벡터에 대한 평균 손실을 나타내는 스칼라 값을 반환한다. 손실이 낮을수록 네트워크의 성능이 향상된다.

손실 함수를 최소화하기 위해서는 네트워크의 출력을 실제 출력에 최대한 가깝게 만드는 네트워크의 매개변수 W1, b1, W2, b2 의 최적값을 찾아야 한다. 이를 위해서 경사하강법(gradient descent)이라는 기법을 사용하는데, 다음과 같은 단계를 포함한다.

  1. 네트워크의 매개 변수를 무작위로 초기화한다.
  2. 순방향 패스를 수행하여 네트워크의 출력과 손실 함수를 계산한다.
  3. 백워드 패스를 수행하여 네트워크의 파라미터에 대한 손실 함수의 기울기를 계산한다.
  4. 현재 값에서 기울기의 일부를 빼서 네트워크의 매개변수를 업데이트한다.
  5. 손실 함수가 최소값에 도달하거나 수렴 기준이 충족될 때까지 2~4단계를 반복한다.

함수의 기울기는 함수의 가장 가파른 오르막길 방향을 가리키는 벡터이다. 네트워크의 매개변수에 대한 손실 함수의 기울기는 우리가 매개변수를 소량씩 변경할 때 손실 함수가 얼마나 변하는지 알려준다. 현재 값에서 기울기의 일부를 빼서 매개변수를 기울기의 반대 방향, 즉 손실함수의 가장 가파른 하강 방향으로 이동시킨다. 이렇게 하면 손실함수를 점진적으로 줄이고 네트워크의 성능을 향상시킬 수 있다.

현재 값에서 기울기를 차감한 비율을 학습률이라고 하는데, 이는 네트워크가 얼마나 빨리 학습하는지 또는 느리게 학습하는지를 결정한다. 학습률이 높으면 학습 과정이 빨라질 수 있지만, 네트워크가 최소값을 초과하여 발산할 수도 있다. 학습률이 낮으면 네트워크가 발산하는 것을 막을 수 있지만, 학습 과정이 느려지고 로컬 최소값에 갇힐 수도 있다. 신경망 훈련에서 적절한 학습률을 선택하는 것은 중요하고 어려운 작업이다.

역방향 단계(pass)는 역전파 알고리즘의 가장 중요하고 복잡한 부분이다. 이것은 네트워크의 매개변수에 대한 손실 함수의 기울기를 계산하기 위해 미적분학의 연쇄 법칙(chain rule)을 적용하는 것을 포함한다. 연쇄 법칙은 합성 함수의 기울기를 더 간단한 성분의 기울기의 곱으로 분해할 수 있게 해준다. 예를 들어, 함수 \(h(x) = f(g(x))\)를 가질 때, \(x\)에 대한 \(h\)의 기울기는 \(g\)에 대한 \(f\)의 기울기와 \(x\)에 대한 \(g\)의 기울기의 곱이다. 공식은: \(h'(x) = f'(g(x)) * g'(x)\)이다.

피드포워드 신경망의 경우 손실 함수는 네트워크의 매개 변수와 활성화 함수의 합성 함수이다. 따라서 체인 규칙을 사용하여 네트워크의 출력에 대한 손실 함수의 기울기, 출력 레이어 입력에 대한 네트워크 출력의 기울기, 히든 레이어 출력에 대한 출력 레이어 입력의 기울기 등을 곱하여 네트워크의 매개 변수에 대한 손실 함수의 기울기를 계산할 수 있다. 이 과정은 출력 레이어에서 시작하여 네트워크를 통해 역방향으로 이동하여 레이어별로 기울기를 계산하기 때문에 역전파라고 한다.

다음 절에서는 Python에서 역전파 알고리즘을 구현하는 방법을 살펴보고 이를 적용하여 간단한 피드포워드 신경망을 훈련시킨다.

역전파의 동작

이 절에서는 입력 레이어 하나, 은닉 레이어 하나, 출력 레이어 하나로 구성된 간단한 네트워크의 예를 따라 역전파가 어떻게 작동하는지 설명한다. 또한 네트워크의 학습 과정과 매개 변수 업데이트를 설명하는 데 사용되는 수학적 표기법과 공식도 설명한다.

역전파 알고리즘은 피드포워드 신경망이 데이터로부터 학습하고 그에 따라 매개변수를 조정할 수 있도록 하는 알고리즘이다. 네트워크 출력의 오류, 즉 손실을 계산하여 네트워크를 통해 역전파하고, 그 과정에서 각 뉴런의 가중치와 편향을 업데이트한다는 개념이다. 역전파는 미적분학의 연쇄 법칙을 응용한 것으로, 복잡한 함수의 도함수를 단순한 구성 요소의 도함수를 곱하여 계산할 수 있다.

이 포스팅에서 사용할 몇 가지 기호와 변수를 정의하는 것부터 시작하겠다.

- \(L\): 입력 레이어를 제외한 네트워크의 레이어의 갯수이며 우리 예에서는 \(L = 2\).

- \(J\): 네트워크의 비용 함수이며, 네트워크의 결과 값과 참 출력 값 간의 차이를 측정한다. 비용 함수는 평균 제곱 오차, 교차 엔트로피 또는 로그 손실 같이 오류를 정량화하는 함수이다. 예에서 교차 엔트로피 비용함수를 사용하며, 다음과 같이 정의한다.

\[J = - \cfrac{1}{m}\sum_{i=1}^{m}\sum_{j=1}^{n_y} y_{ij}log{\hat{y}_{ij}}\]

이째 \(m\)은 데이터 세트에서 샘플의 갯수이며, \(n_y\)는 출력 뉴런 또는 클래스의 수이며, \(y_{ij}\)는 \(j\)번째 출력 뉴런의 \(i\)번째 예시의 실제 레이블 또는 클래스이고, \(\hat{y_{ij}}\)는 \(j\)번째 출력 뉴런의 \(i\)번째 예시의 예측 확률이다.

- \(\cfrac{\partial J}{\partial{W^{[l]}}}\): 네트워크의 레이어 \(l\)의 가중치 행렬에 대한 비용 함수의 기울기로 이때 여기 예에서는 \(l\) 1 또는 2이다. 기울기는 가중치 행렬 (\(n^{[l]}\), \(n^{[l-1]}\))이며, 이때 \(n^{[l]}\)는 레이어 \(l\)에서 뉴런의 수이며, \(n^{[l-1]}\)은 이전 레이어에서 뉴런의 수이다. 기울기는 가중치 행렬을 약간 변경할 때 비용 함수 변화량을 보인다.

- \(\cfrac{\partial J}{\partial{b^{[l]}}}\): 네트워크에서 \(l\) 에이어의 편향 벡터에 대한 비용 함수의 기울기, 이때 예에서 \(l\)의 값은 1 또는 2이다. 기울기는 편향 벡터 (\(n^{[l]}\), 1)와 동일한 차원의 벡터이며, 이때 \(n^{[l]}\)은 \(l\) 레이어에서 뉴런의 갯수이다. 편향 벡터을 변경하면, 기울기는 비용 함수의 변화량을 보인다.

- \(\cfrac{\partial J}{\partial{Z^{[l]}}}\): 네트워크에서 \(l\) 에이어의 선형 결합에 대한 비용 함수의 기울기, 이때 예에서 \(l\)의 값은 1 또는 2이다. 기울기는 선형 결합 (\(n^{[l]}\), m)와 동일한 차원의 행렬이며, 이때 \(n^{[l]}\)은 \(l\) 레이어에서 뉴런의 갯수이며, \(m\)은 데이터 세트에서 샘플 또는 예의 갯수이다. 선형 결합을 변경하면, 기울기는 비용 함수의 변화량을 보인다.

- \(\cfrac{\partial J}{\partial{A^{[l]}}}\): 네트워크에서 \(l\) 에이어의 활성화 출력에 대한 비용 함수의 기울기, 이때 예에서 \(l\)의 값은 1 또는 2이다. 기울기는 활성화 출력 (\(n^{[l]}\), m)와 동일한 차원의 행렬이며, 이때 \(n^{[l]}\)은 \(l\) 레이어에서 뉴런의 갯수이며, \(m\)은 데이터 세트에서 샘플 또는 예의 갯수이다. 활성화 출력을 변경하면, 기울기는 비용 함수의 변화량을 보인다.

- \(\alpha\): 네트워크의 학습률, 이는 매개변수를 업데이트할 때 스텝의 변화를 결정한다. 학습률은 사용자가 선택할 수 있는 양의 스칼라 갑이다. 적은 학습률은 네트워크가 학습을 천천히 하는 것을 의미하지만, 보다 정확할 수 있다. 반대로 큰 학습률은 네트워트가 보다 빠르게 학습한다는 것을 뜻하지만, 덜 안정적이다.

이 기호들과 변수들을 이용하여 역전파 알고리즘의 일반적인 공식을 작성할 수 있다. 역전파 알고리즘은 각 레이어에 대해 다음과 같은 두 단계로 구성된다.

- Step 1: 레이어의 선형 결합에 대한 비용 함수의 기울기를 계산한다.

\[\cfrac{\partial J}{\partial{Z^{[l]}}} = {\cfrac{\partial J}{\partial{A^{[l]}}}} {\cfrac{\partial A^{[l]}}{\partial{Z^{[l]}}}} \]

- Step 2: 레이어의 매개변수에 대한 비용 함수의 기울기를 계산한다.

\[\cfrac{\partial J}{\partial{W^{[l]}}} = {\frac{1}{m}}{\cfrac{\partial J}{\partial{Z^{[l]}}}}{A^{[l-1]T}}$$ $$\cfrac{\partial J}{\partial{b^{[l]}}} = {\frac{1}{m}}{\sum_{i=1}^m{\cfrac{\partial J}{\partial{Z^{[l]}}_i}}} \]

최중 레이어에서는 비용 함수 자신의 미분 \(\cfrac{\partial J}{\partial{\hat {y}}}\)는 레이어의 활성화 출력 \(\cfrac{\partial J}{\partial{A^{[L]}}}\)에 대한 비용 함수의 기울기를 갖는다. 이전 레이어들에서는 레이어의 활성화 출력 \(\cfrac{\partial J}{\partial{A^{[l]}}}\)에 대한 비용 함수의 기울기는 다음 레이어의 선형 결합에 대한 비용 함수의 기울기 \(\cfrac{\partial J}{\partial{Z^{[l+1]}}}\)과 다음 레이어의 가중치 행렬의 \(W^{[l+1]}\)의 곱이다.

각 레이어의 기울기를 계산한 후 다음 공식을 사용하여 네트워크의 매개변수를 업데이트할 수 있다.

\[W^{[l]} = W^{[l]} - {\alpha}{\cfrac{\partial J}{\partial{W^{[l]}}}}\]
\[b^{[l]} = b^{[l]} - {\alpha}{\cfrac{\partial J}{\partial{b^{[l]}}}}\]

비용 함수가 최소값에 이르거나 주어진 반복 횟수 또는 에포크 수에 다다를 때까지 이 식을 반복적으로 적용한다.

이제 입력 레이어 하나, 은닉 레이어 하나와 출력 레이어 하나로 이루어진 네트워크 예에 공식을 적용하여 보자. 이전 절의 동일한 입력 행렬 \(X\)와 출력 행렬 \(y\)을 사용한다. 또한 이전 절에서 정의한 동일한 가중치 행렬 \(W^{[1]}\)과 \(W^{[2]}\) 그리고 편향 벡터 \(b^{[1]}\)과 \(b^{[2]}\)를 사용할 것이다. 은닉 레이어를 위하여 sigmoid 활성화 함수를 그리고 출력 레이어를 위하여 softmax 활성화 함수를 사용한다. 그리고 힉습률로는 0.01을 선택한다.

다음 코드는 Python에서 역전파 알고리즘의 한 번 반복을 수행하는 방법을 보이고 있다.

# Import the libraries
import numpy as np
import matplotlib.pyplot as plt

# Define the network architecture
n_x = 2 # Number of input neurons
n_h = 3 # Number of hidden neurons
n_y = 2 # Number of output neurons

# Define the network parameters
W1 = np.random.rand(n_x, n_h) # Weights from input to hidden layer
b1 = np.random.rand(n_h) # Biases of hidden layer
W2 = np.random.rand(n_h, n_y) # Weights from hidden to output layer
b2 = np.random.rand(n_y) # Biases of output layer

# Define the activation functions
def sigmoid(x):
    # Sigmoid function
    return 1 / (1 + np.exp(-x))

def softmax(x):
    # Softmax function
    exp_x = np.exp(x)
    return exp_x / np.sum(exp_x, axis=1, keepdims=True)

# Define the input data
X = np.array([[0, 0], [0, 1], [1, 0], [1, 1]]) # Input data matrix
y = np.array([[0, 1], [1, 0], [1, 0], [0, 1]]) # Output data matrix

# Define the loss function
def cross_entropy(y_true, y_pred):
    # Cross-entropy function
    return -np.sum(y_true * np.log(y_pred))

# Define the learning rate
alpha = 0.1

# Define the number of epochs
epochs = 100

# Define the list to store the loss values
loss_values = []

# Loop over the epochs
for epoch in range(epochs):
    # Forward pass
    Z1 = X.dot(W1) + b1 # Linear combination from input to hidden layer
    A1 = sigmoid(Z1) # Activation at hidden layer
    Z2 = A1.dot(W2) + b2 # Linear combination from hidden to output layer
    A2 = softmax(Z2) # Activation at output layer
    # Backward pass
    dZ2 = A2 - y # Gradient at output layer
    dW2 = A1.T.dot(dZ2) # Gradient at W2
    db2 = np.sum(dZ2, axis=0) # Gradient at b2
    dZ1 = dZ2.dot(W2.T) * A1 * (1 - A1) # Gradient at hidden layer
    dW1 = X.T.dot(dZ1) # Gradient at W1
    db1 = np.sum(dZ1, axis=0) # Gradient at b1
    # Weight update
    W2 = W2 - alpha * dW2 # Update W2
    b2 = b2 - alpha * db2 # Update b2
    W1 = W1 - alpha * dW1 # Update W1
    b1 = b1 - alpha * db1 # Update b1
    # Compute the loss
    loss = cross_entropy(y, A2)
    # Print the loss every 10 epochs
    if epoch % 10 == 0:
        print(f"Epoch {epoch}, loss {loss}")
    # Append the loss to the list
    loss_values.append(loss)

# Plot the loss values
plt.plot(loss_values)
plt.xlabel("Epoch")
plt.ylabel("Loss")
plt.show()

역전파가 중요한 이유

역전파는 피드포워드 신경망이 데이터로부터 학습하고 성능을 향상시킬 수 있는 핵심 알고리즘이기에 중요하다. 역전파가 없었다면 신경망은 매개변수를 조정하고 오류를 줄일 수 없었을 것이고, 무작위이며 비효율적인 가중치와 편향에 갇혀 있었을 것이다. 역전파는 데이터를 신경망에 적응하고 손실 함수를 최소화하는 매개변수의 최적 값을 찾을 수 있도록 한다.

역전파는 구조나 활성화 함수, 손실 함수에 관계없이 모든 피드포워드 신경망에 적용할 수 있는 일반적이고 강력한 알고리즘이기에 중요하다. 역전파는 여러 개의 은닉 레이어, 여러 종류의 뉴런이 있는 네트워크와 회귀, 분류, 클러스터링 등 다양한 종류의 문제를 처리할 수 있다. 역전파는 미적분학의 연쇄 법칙에 기반을 두고 있으며, 이 규칙은 모든 복합 함수의 도함수를 계산할 때 사용할 수 있는 보편적이고 간단한 규칙이다.

역전파는 컨볼루션 신경망, 순환 신경망, 딥 러닝과 같은 많은 고급 현대 신경망 기술의 기초이기 때문에 중요하다. 이러한 기술은 역전파를 핵심 알고리즘으로 사용하여 네트워크를 훈련하고 컴퓨터 비전, 자연어 처리, 음성 인식과 같은 다양한 영역에서 최첨단 결과를 달성한다. 역전파는 이러한 다양하고 복잡한 신경망 모델을 연결하는 공통 고리이다.

요약하면 역전파가 중요한 이유는 피드포워드 신경망을 학습, 적응 및 수행하도록 하는 알고리즘이기 때문이다. 역전파는 신경망 훈련의 본질이자 많은 신경망 응용의 기본이다.

역전파의 과제와 한계

역전파는 피드포워드 신경망이 데이터를 통해 학습하고 성능을 향상시킬 수 있는 강력하고 일반적인 알고리즘이다. 그러나 역전파도 해결해야 할 과제와 한계가 있다. 이 절에서는 역전파의 공통적인 과제와 한계, 그리고 이를 어떻게 처리해야 하는지에 대해 논의할 것이다.

역전파의 주요 과제 중 하나는 네트워크와 학습 과정에 적합한 하이퍼파라미터를 선택하는 것이다. 하이퍼파라미터는 네트워크에 의해 학습되지 않고, 학습 전에 사용자에 의해 설정되는 파라미터이다. 중요한 하이퍼파라미터 중 일부는 다음과 같다.

  • 은닉 레이어의 수와 크기, 뉴런들의 타입과 수, 활성화 함수들과 같은 네트워크 아키텍처
  • 네트워크가 얼마나 빨리 학습하는지 또는 느리게 학습하는지를 결정하는 학습 속도(학습률)
  • 네트워크가 훈련하는 시간을 결정하는 에포크 수
  • 한 번에 처리되는 입력 벡터의 수를 결정하는 배치 크기
  • 손실 함수에 페널티 항을 추가하여 네트워크가 데이터를 과적합하는 것을 방지하는 정규화 기법

적절한 하이퍼파라미터를 선택하는 것은 사소한 일이 아니며, 많은 시행착오, 실험 및 평가를 필요로 한다. 하이퍼파라미터를 설정하는 보편적인 공식이나 규칙은 없으며, 문제의 유형과 복잡성, 데이터의 크기와 품질, 사용 가능한 계산 자원에 따라 달라진다. 최적의 하이퍼파라미터를 찾기 위한 일반적인 접근법은 그리드 검색이나 무작위 검색을 사용하는 것으로, 하이퍼파라미터의 다양한 조합을 테스트하고 검증 세트에서 최고의 성능을 달성하도록 선택하는 것을 포함한다.

역전파의 또 다른 과제는 기울기 소실 문제(vanishing gradient problem)와 기울기 폭발 문제(exploding gradient problem) 같은 기울기 관련 문제를 다루는 것이다. 이러한 문제는 네트워크의 매개변수에 대한 손실 함수의 기울기가 너무 작거나 커져 네트워크가 학습을 중단하거나 분기할 때 발생한다. 기울기 소실 문제는 기울기가 네트워크를 통해 역 전파됨에 따라 점점 더 작아질 때, 특히 네트워크에 많은 숨겨진 레이어가 있고 시그모이드 함수와 같이 포화되는 활성화 함수를 사용할 때 발생한다. 기울기 폭발 문제는 기울기가 네트워크를 통해 역 전파됨에 따라 점점 더 커질 때, 특히 네트워크에 큰 가중치와 편향이 있고 선형 함수와 같이 포화되지 않는 활성화 함수를 사용할 때 발생한다.

기울기와 관련된 문제를 처리하는 다음과 같은 몇 가지 방법이 있다.

  • 양의 입력에 대해 1의 일정한 기울기를 갖고 음의 입력에 대해 0의 기울기를 갖는 정류된 ReLU 함수와 같이 포화되지(saturate) 않는 활성화 함수를 사용한다.
  • 레이어의 크기에 따라 가중치와 바이어스를 스케일링하는 Xavier 초기화 또는 He 초기화와 같은 가중치와 바이어스가 너무 크거나 작은 것을 방지하는 가중치 초기화 기술을 사용한다.
  • 기울기의 크기를 노름 클리핑(norm clipping) 또는 값 클리핑(vlaue clipping) 같이 특정 임계값으로 제한하는 기울기 클리핑 기술을 사용하여 기울기가 특정 노름 또는 값을 초과하지 않도록 한다.
  • 배치 정규화(batch normalization) 레이어와 같이 각 레이어의 입력이 제로 평균과 단위 분산을 갖도록 정규화하는 배치 정규화 기술을 사용하여 내부 공변량(covariate) 이동을 줄이고 기울기의 안정성을 향상시킨다.

역전파의 세 번째 과제는 손실 함수가 영의 기울기를 가지지만 반드시 최소값이 아닌 점인 로컬 최소값과 안장점(saddle point)을 다루는 것이다. 로컬 최소값은 손실함수가 이웃하는 점들보다 낮은 값을 가지지만 전체 도메인에서 가장 낮은 값을 가지는 것은 아니다. 안장점은 손실 함수가 어떤 방향에서는 영의 기울기를 갖지만 모든 방향에서는 그렇지 않은 점이다. 로컬 최소값과 안장점 모두 네트워크를 가두어 전체 도메인에서 손실 함수가 가장 낮은 값인 글로벌 최소값에 도달하지 못할 수 있다.

로컬 최소값과 안장점을 처리하는 방법으로 다음과 같은 것이 있다.

  • 미니 배치 경사 하강법(mini-batch gradient descent) 또는 온라인 경사 하강법(online gradient descent) 같은 전체 데이터가 아닌 입력 데이터의 무작위 부분 집합을 사용하여 네트워크의 매개 변수를 업데이트하는 확률적 경사 하강 기술(stochastic gradient descent technique)을 사용하여 기울기에 약간의 노이즈와 가변성을 도입하고 네트워크가 로컬 최소값과 안장점에서 탈출하도록 돕는다.
  • 모멘텀 방식이나 Nesterov 가속 기울기 방식과 같이 현재의 기울기만을 사용하는 것이 아니라, 현재의 업데이트 이전 업데이트의 일부를 추가하는 모멘텀 기법을 사용하는 것이 가장 가파른 하강 방향을 따라 네트워크의 이동을 가속화하고 네트워크가 로컬 최소점과 안장점을 극복할 수 있도록 지원한다.
  • 각 파라미터별로 학습률을 최적화하고 네트워크가 보다 빠르고 효율적으로 수렴할 수 있도록 돕는 AdaGrad, RMSProp 및 Adam 방법과 같이 고정된 학습률을 사용하는 것이 아니라 기울기의 크기와 방향에 따라 학습률을 조절하는 적응형 학습률 기법을 사용한다.

위의 설명은 역전파의 공통적인 과제와 한계, 그리고 이를 어떻게 처리할 것인지에 대한 몇 가지 방안이다. 그러나 역전파는 여전히 피드포워드 신경망 훈련과 다양한 문제 해결에 매우 효과적이고 널리 사용되는 알고리즘이다. 역전파는 많은 신경망 기술과 응용 분야의 중추이며, 연구자와 실무자들에 의해 끊임없이 개선되고 정교화되고 있다.

요약

이 포스팅에서는 피드포워드 신경망과 역전파의 작동 방식에 대해 배웠다. 뉴런, 가중치, 편향, 활성화 함수, 손실 함수 등 신경망의 기본 개념과 용어에 대해 설명하였다. Python에서 간단한 피드포워드 신경망을 구현하고 이를 사용하여 이진 분류 문제를 해결하는 방법에 대해 보였다. 역전파 알고리즘을 사용하여 네트워크의 매개 변수에 대한 손실 함수의 기울기를 계산하고 기울기 하강 기법을 사용하여 업데이트하는 방법에 대해서도 다루었다. 역전파의 일반적인 과제와 한계, 그리고 이에 대처하는 방법에 대해서도 논의하였다.

피드포워드 신경망과 역전파는 많은 문제와 영역에 적용할 수 있는 강력하고 일반적인 기술이다. 이들은 컨볼루션 신경망, 순환 신경망, 딥 러닝 등 많은 고급 및 현대 신경망 모델의 기반이다. 피드포워드 신경망과 역전파의 작동 방식을 이해하면 신경망 훈련과 응용의 내부 작동과 원리에 대해 더 깊이 이해할 수 있다.